The floorz function uses zero fuzzing.
Floor function in sas example.
If you compute the difference however you can see that the values are different.
The floor function fuzzes the results so that if the results are within 1e 12 of an integer the floor function returns that integer.
Functions that create sas date datetime and time values the first three functions in this group of functions create sas date values datetime values and time values from the constituent parts month day year hour minute second.
For example and while.
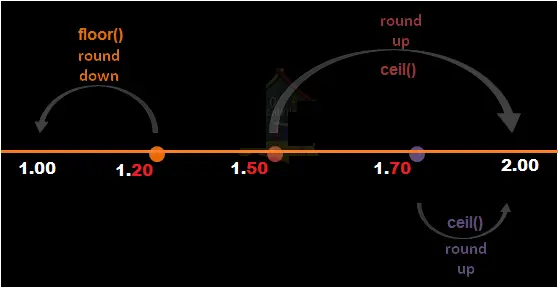
Round down in sas or floor in sas uses floor function which rounds down the column in sas.
Round up or ceil in sas using ceil function.
The floor function fuzzes the results so that if the results are within 1e 12 of an integer the floor function returns that integer.
Some say int 3 65 4 the same as the floor function.
The mdy function can create a sas date value given a value for the month day and year.
If x is your number the sas statement looks like this y 100 floor x 100.
Therefore with the floorz function you might get unexpected results.
Round down to nearest 100.
Multiply the result by 100 to restore the scale of the original number.
Round off the column in sas is accomplished by round function.
If the argument is within 1e 12 of an integer the floor function fuzzes the result to be equal to that integer.
The floorz function uses zero fuzzing.
Let s see an example of each.
Unlike the floorz function the floor function fuzzes the result.
Round up in sas or ceil in sas uses ceil function which rounds up the column in sas.
And this is the ceiling function.
Now let s get started.
For example the decimal values 0 1 and 0 3 do not have exact binary representations.
The int function short for integer is like the floor function but some calculators and computer programs show different results when given negative numbers.
Therefore with the floorz function you might get unexpected results.
The floorz function does not fuzz the result.
In mathematics and computer science the floor function is the function that takes as input a real number and gives as output the greatest integer less than or equal to denoted or similarly the ceiling function maps to the least integer greater than or equal to denoted or.